BAB 1 : EKSPONEN

Fungsi Eksponen

Pada pembahasan ini kita akan mempelajari fungsi eksponensial. Misalnya,

merupakan fungsi eksponensial yang memiliki basis 2. Perhatikan bahwa fungsi ini naik/bertambah dengan sangat cepat.

Jika kita bandingkan fungsi ini dengan fungsi g(x) = x² yang menghasilkan g(30) = 900, kita dapat melihat bahwa jika variabel fungsi berada dalam eksponen, maka perubahan kecil pada variabel akan menyebabkan perubahan yang dramatis dalam nilai fungsi.

Fungsi Eksponensial

Untuk mempelajari fungsi eksponensial, pertama kita harus mendefinisikan apa yang dimaksud dengan bentuk eksponensial ax dengan x adalah sebarang bilangan real. Dalam pembahasan ini kita sudah tahu definisi ax untuk a > 0 dan x adalah bilangan rasional, yaitu

Akan tetapi bagaimana jika x adalah bilangan irasional? Berapakah nilai dari 5√3 atau 2π? Untuk mendefinisikan ax ketika x adalah bilangan irasional, kita dekati x dengan menggunakan bilangan rasional.

Misalkan, karena

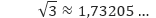
merupakan bilangan irasional, kita dapat mendekati a√3 dengan barisan pangkat bilangan rasional berikut:

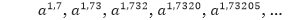
Secara intuitif, kita dapat melihat bahwa pangkat rasional dari a akan mendekat dan terus mendekat ke a√3. Dapat ditunjukkan dengan menggunakan matematika lanjut bahwa terdapat tepat satu bilangan yang didekati oleh barisan tersebut. Kita definisikan a√3sebagai bilangan ini.

Misalkan, dengan menggunakan kalkulator, kita dapat menghitung

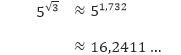
Semakin banyak desimal yang kita gunakan untuk menentukan √3 dalam perhitungan, maka kita akan mendapatkan pendekatan yang semakin baik.

---

Definisi Fungsi Eksponensial

Fungsi eksponensial f dengan basis a dinotasikan dengan

di mana a > 0, a ≠ 1, dan x merupakan sebarang bilangan real.

---

Kita menganggap bahwa a ≠ 1 karena fungsi f(x) = 1x = 1 merupakan fungsi konstan. Berikut ini beberapa contoh fungsi eksponensial:

Contoh 1: Menentukan Nilai Fungsi Eksponensial

Gunakan kalkulator untuk menentukan nilai masing-masing fungsi berikut pada x yang diberikan.

1. f(x) = 2x pada x = –3,1
2. f(x) = 2–x pada x = π
3. f(x) = 0,6x pada x = 3/2.

Pembahasan

1. f(–3,1) = 2–3,1 ≈ 0,1166291
2. f(π) = 2–π ≈ 0,1133147
3. f(3/2) = (0,6)3/2 = 0,4647580

Ketika menghitung nilai fungsi eksponensial dengan menggunakan kalkulator, selalu ingat untuk menutup eksponen yang berbentuk pecahan dalam tanda kurung. Hal ini dikarenakan kalkulator mengikuti urutan operasi, dan tanda kurung sangat penting untuk mendapatkan hasil yang benar.