Trigonometri
Pengertian Trigonometri
Trigonometri atau kalau dilihat dari bahasa Yunani yaitu trigonon = “tiga sudut” dan metron = “mengukur” ialah sebuah cabang ilmu matematika yang mempelajari hubungan yang meliputi panjang dan sudut segitiga. Dimana trigonometri ini muncul pada abad ke-3 SM (Sebelum Masehi) di masa hellenistik guna mempelajari tentang astronomi
Lalu konsep dasar trigonometri matematika
ialah konsep kesebangunan segitiga siku – siku dan sisi – sisi yang
bersesuaian pada dua bangun datang sebangun yg mempunyai perbandingan
yang sama. Pada konsep geometri euclid sendiri
masing – masing sudut pada dua segitiga memiliki besar yang sama, maka
kedua Segitiga tersebut pasti sebangun dan konsep ini merupakan dasar
untuk perbandingan trigonometri sudut lancip, didalam konsep
trigonometri matematika konsep tersebut telah dikembangkan lagi untuk
sudut – sudut non lancip atau sudut yang lebih dari 90 derajat dan
kurang dari NOL derajat. Konsep dasar trigonometri ini juga berhubungan
dengan tabel sin cos tan yang telah di bahas sebelumnya.
Rumus Trigonometri
Sedangkan rumus trigonometri matematika ini sangat – sangat penting
sekali, khususnya untuk para pelajar siswa dan siswi tingkat SMA
(Sekolah Menengah Atas) di Indonesia karena trigonometri ini sering
muncul di soal – soal Ujian baik itu didalam UAS (Ujian Akhir Sekolah)
maupun didalam UN (Ujian Nasional) tingkat SMA di seluruh Indonesia
sehingga kalian sebagai Siswa Siswi diharapkan dapat memahami tentang
rumus dasar trigonometri matematika ini agar anda bisa mengerjakan soal –
soal tentang trigonometri yang ada didalam UAS dan UN tersebut.
Fungsi Trigonometri dan Rumus Trigonometri Matematika
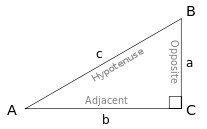
Kemudian di dalam trigonometri matematika mempunyai tiga fungsi yang
pertama ialah sinus yang merupakan perbandingan sisi segitiga (segitiga
siku – siku atau salah satu sudut segitiga itu 90°) yang ada di depan
sudut dengan sisi miring, lalu fungsi trigonometri kedua ialah kosinus
atau cosinus yang merupakan perbandingan sisi segitiga yang terletak
disudut dengan sisi miring dan fungsi dasar trigonometri matematika yang
ketiga ialah tangen yang merupakan perbandingan sisi segitiga yang ada
di depan sudut dengan sisi segitiga yang terletak disudut.
Rumus Fungsi Trigonometri Matematika
Rumus Identitas Trigonometri Matematika
Rumus Jumlah dan Selisih Sudut Trigonometri
Rumus Perkalian Trigonometri Matematika
Rumus Jumlah dan Selisih Trigonometri
Rumus Sudut Rangkap Dua dan Tiga Trigonometri
Rumus Setengah Sudut Trigonometri
Contoh Soal Trigonometri
1. Tentukan lah nilai dari: 2 cos 75° cos 15°
Pembahasan :
Dari soal diatas dapat disimpulkan bahwa jenis soal diatas merupakan
contoh soal perkalian trigonometri maka kita bisa melihat rumus
trigonometri perkalian cos pada uraian diatas yaitu rumusnya adalah 2 cos A cos B = cos (A + B) + cos (A- B)
Jawaban :
nilai 2 cos 75° cos 15° = cos (75 +15)° + cos (75 – 15)°
= cos 90° + cos 60°
= 0 + ½
= ½
= cos 90° + cos 60°
= 0 + ½
= ½
Maka nilai dari 2 cos 75° cos 15° yaitu ½
2. Tentukan lah nilai dari sin 105° + sin 15°
Pembahasan :
Dari soal diatas dapat disimpulkan bahwa jenis soal diatas merupakan
contoh soal penjumlahan trigonometri maka kita bisa melihat rumus
trigonometri penjumlahan sin pada uraian diatas yaitu rumusnya adalah 2sin ½ (A+B) cos ½ (A-B)
Jawaban :
nilai sin 105° + sin 15° = 2 sin ½ (105+15)°cos ½ (105-15)°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°
Maka nilai dari sin 105° + sin 15° adalah sin 60° cos 45°
Mungkin hanya seperti itu saja pembahasan tentang rumus trigonometri
matematika yang telah kami ulas dan tulis secara lebih lengkap, semoga
saja apa yang sudah kami tulis tentang rumus dasar trigonometri
matematika tersebut bisa dipahami dengan mudah oleh kalian dan semoga
saja berguna bagi kalian sebagai seorang pelajar di tingkat sekolah
menengah atas (SMA), lalu sebagai tambahan saja bahwa referensi kami
dalam menulis ini diambil dari buku pelajar matematika tingkat sma
sehingga sudah bisa dipercaya kebenaran rumusnya.

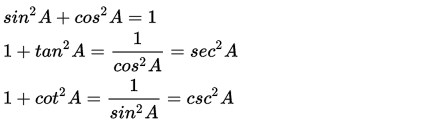

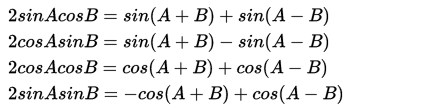
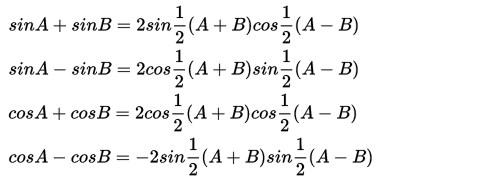
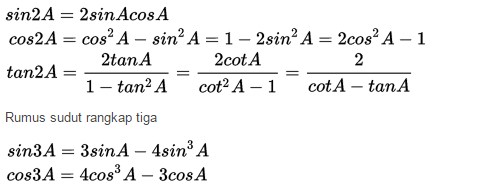











0 comments:
Post a Comment