TUGAS 2 MAT. MINAT SMT 2

11.    Diketahui titik A(1, -2, -8) dan titik B(3, -4, 0). Titik P terletak pada perpanjangan AB sehingga 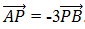Jika b ⃗ merupakan vektor posisi titik P, maka p ⃗ = ...

PEMBAHASAN:
Mari kita ilustrasikan soal tersebut dalam gambar:


JAWABAN: A

12.    Jika besar sudut antara vektor p ⃗ dan vektor q ⃗ adalah 60 derajat, panjang p ⃗ dan q ⃗ masing-masing 10 dan 6, maka panjang vektor p ⃗ - q ⃗ = ... 
a.    4
b.    9
c.    14
d.    2√17
e.    2√19
PEMBAHASAN:
Panjang vektor p ⃗ - q ⃗ adalah:

JAWABAN: E

13.   
a.    4
b.    2
c.    1
d.    0
e.    -1
PEMBAHASAN:


JAWABAN: D

14.    Agar vektor a = 2i + pj + k dan b = 3i + 2j + 4k saling tegak lurus, maka nilai p adalah...
a.    5
b.    -5
c.    -8
d.    -9
e.    -10
PEMBAHASAN:
Vektor a dan b saling tegak lurus, maka a . b = 0
a . b = 0
2(3) + p(2) + 1(4) = 0
6 + 2p + 4 = 0
2p = -10
p = -5
JAWABAN: B

15.    Vektor yang merupakan proyeksi vektor (3, 1, -1) pada (2, 5, 1) adalah ...
a.    3/10 (2, 5, 1)
b.    3 (3, 1, -1)
c.    1/30 (2, 5, 1)
d.    1/3 (2, 5, 1)
e.    1/3 (2, 5, -1)
PEMBAHASAN:
Rumus untuk mencari proyeksi vektor a ⃗ dan b ⃗ adalah:

JAWABAN: D

16.    Nilai p agar vektor pi + 2j – 6k dan 4i – 3j + k saling tegak lurus adalah ...
a.    6
b.    3
c.    1
d.    -1
e.    -6
PEMBAHASAN:
Agar saling tegak lurus maka hasil kali kedua vektor tersebut haruslah nol.
( pi + 2j – 6k ) . ( 4i – 3j + k ) = 0
p(4) + 2 (-3) + (-6)(1) = 0
4p – 6 – 6 = 0
4p – 12 = 0
4p = 12
p = 3
JAWABAN: B

17.    

 PEMBAHASAN:

JAWABAN: D

18.    Diketahui titik A (5, 1, 3); B (2, -1, -1) dan C (4, 2, -4). Besar <ABC adalah ...
a.    π
b.    π/2
c.    π/3
d.    π/6
e.    0
PEMBAHASAN:
(AB) ̅ = (2 – 5, -1 – 1, -1 – 3) = (-3, -2, -4)
(CB) ̅ = (2 – 4, -1 – 2, -1 – (-4)) = (-2, -3, 3)
Besar <ABC adalah:

JAWABAN: B

19.    Diketahui vektor  ⃗tegak lurus terhadap v ⃗maka nilai a adalah ...
a.    -1
b.    -1/3
c.    1/3
d.    1
e.    3
PEMBAHASAN:

     (6 – 3a)3 + (4 – 9a) 9 + (-2 + 12a)(-12) = 0
     (18 – 9a) + (36 – 81a) + (24 – 144a) = 0
     18 + 36 + 24 -9a – 81a – 144a = 0
     78 – 234a = 0
     234a = 78
     a = 78/234
     a = 1/3
JAWABAN: C

20.    Jika maka tan θ adalah ...
a.    3/5
b.    ¾
c.    4/3
d.    9/16
e.    16/9
PEMBAHASAN:

tan θ = 3/4 , ingat segitiga siku-siku

JAWABAN: B